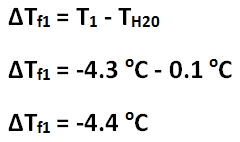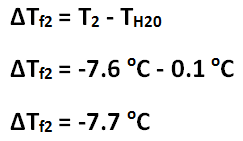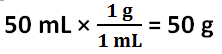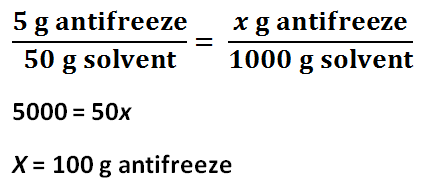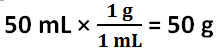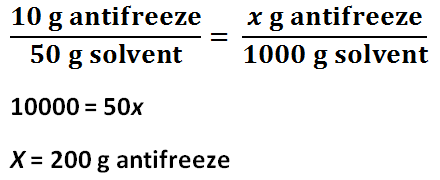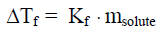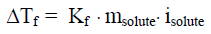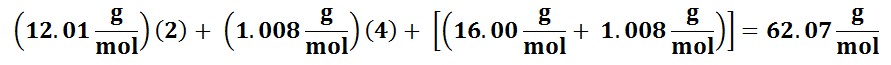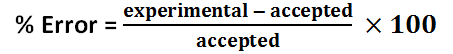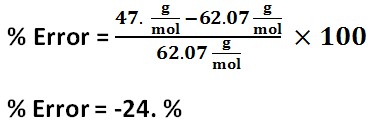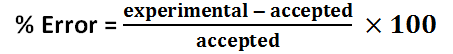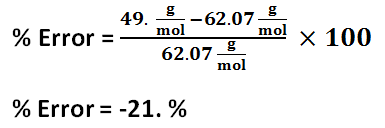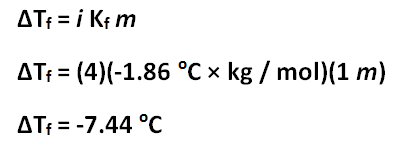Freezing Point Depression with Anitfreeze Lab
Purpose: to determine the freezing point depression of antifreeze solutions - used to lower the freezing point of water in the cooling systems of automobiles - by cooling them in an ice-salt bath
Data Table
|
freezing point of distilled water (T H2O)
freezing point of Solution 1 (T 1)
freezing point of Solution 2 (T 2)
|
0.1 C
-4.3 C
-7.6 C
|
Calculations
Freezing point depression of Solution 1
Freezing point depression of Solution 2
Molality of Solution 1
Molality of Solution 2
Number of grams of antifreeze per 1000 grams of solvent for Solution 1
Number of grams of antifreeze per 1000 grams of solvent for Solution 2
Molar mass of antifreeze in Solution 1
Molar mass of antifreeze in Solution 2
Conclusion
The freezing point depression of Solution 1 is -4.4 C, and the freezing point depression of Solution 2 is -7.7 C. The freezing point depression can be determined by subtracting the temperature of the solution by the temperature of the water. The molality of Solution 1 is 2.4 mol / kg, and the molality of Solution 2 is 4.1 mol / kg. The molality can be determined by using the freezing point depression equation because the freezing point depression had been previously determined. The number of grams of antifreeze per 1000 grams of solvent for Solution 1 is 100 g, and the number of grams of antifreeze per 1000 grams of solvent for Solution 2 is 200 g. First, the 50 mL must be converted to 50 g. Then, using a proportion, the number of grams of antifreeze per 1000 grams of solvent can be determined. The molar mass of the antifreeze in Solution 1 is 47. g / mol, and the molar mass of the antifreeze in Solution 2 is 49. g / mol. The molar mass can be determined by dividing the number of grams of antifreeze per 1000 grams of solvent by the molality of the solutions. One kilogram is equivalent to 1000 grams, so this mass will cancel out the per kilograms of solvent unit in molality, leaving grams over mole to have the units: grams per mole. The freezing point of Solution 2 was lower than the freezing point of Solution 1 because Solution 2 contained 5 more grams of antifreeze; Solution 2 contained double the amount of antifreeze contained in Solution 1. The molality of Solution 2 was greater than Solution 1 because Solution 2 contained 5 more grams of antifreeze; however, the molar mass of the two solutions are roughly the same because it is the molar mass of the antifreeze itself.
Discussion of Theory
Antifreeze is used in automobile cooling systems; it is added to water in the radiator. The normal freezing temperature of pure water is 0 C, but water containing a solute freezes at lower temperatures. This colligative property of freezing-point depression prevents engines from freezing in subzero temperatures and freezing environments. The equation for finding the change in freezing point (or melting point) of a non-electrolyte solution is:
It shows that the change in freezing point (delta T f) of a solution is dependent on the molality of the solute. The constant K f is the molal-freezing-point-depression constant and is unique to the solvent. For example, the molal-freezing-point-depression constant for water is 1.86 C/molal, whereas the molal-freezing-point-depression constant for benzene is 2.53 C/molal. Therefore, an aqueous solution containing 1.0 molal of any type of solute will freeze at -1.86 C. The freezing-point depression does not depend on what type of particles; it solely depends on how many particles are present. For example, a 1.0 molal aqueous sucrose solution will freeze at the same temperature as a 1.0 molal ethylene glycol solution.
Electrolyte solutions behave in the way. It is important to note that it is not the particle identity that determines the freezing-point depression, but it is the number of particles present that determines the freezing-point depression. For example, a 0.50 molal aqueous sodium chloride solution will freeze at -1.86 C because the solution contains 0.50 molal of sodium ions and 0.50 molal of chlorine ions for a total solute concentration of 1.0 molal. The equation for finding the change in freezing point (or melting point) of an electrolyte solution is:
Electrolyte solutions behave in the way. It is important to note that it is not the particle identity that determines the freezing-point depression, but it is the number of particles present that determines the freezing-point depression. For example, a 0.50 molal aqueous sodium chloride solution will freeze at -1.86 C because the solution contains 0.50 molal of sodium ions and 0.50 molal of chlorine ions for a total solute concentration of 1.0 molal. The equation for finding the change in freezing point (or melting point) of an electrolyte solution is:
The i solute represents the van't Hoff factor (mole of particles in solution/ moles of solute dissolved): 1 for non-electrolytes, 2 for electrolytes such as NaCl, 3 for electrolytes such as MgCl2, 4 for electrolytes such as Fe(NO3)3, and so on. For weak acids and bases, such as HC2H3O2, i solute is 1+ because most of the solute stays together, but a small part of it dissociates. Therefore, the i solute value is a little more than 1, or 1+. For strong acids and bases, such as HCl and HBr, i solute is 2. A unique exception to this rule is H2SO4, where the i solute value is 2+. Almost all of it splits into H ions and HSO4 ions, resulting in two particles, but the HSO4 is a weak ion, so a small part of it dissociates. Therefore, the i solute value of H2SO4 is 2+. The actual values of i solute are less than expected due to clustering (ion pairing); the values for i solute become closer to the expected value the more dilute the solution becomes.
The freezing point of Solution 2 was lower than the freezing point of Solution 1 because Solution 2 contained 5 more grams of antifreeze. In the freezing point depression equation above, nothing is changed on the right-hand side of the equation except for the molality of the solute. The molal-freezing-point-constant and the van't Hoff factor remain the same. The molality changes because the moles of solute is increased. The number of moles can be determined by multiplying the number of grams by the inverted grams per mole value, which would become: grams x (moles / grams). This way, the grams would cancel out, only leaving the number of moles. Due to Solution 2 containing double the amount of grams compared to Solution 1, the moles of antifreeze in Solution 2 would be double the moles of antifreeze in Solution 1; therefore, because molality is calculated by dividing the number of moles of the solute by the mass of the solvent in kilograms, Solution 2 has a greater molality than Solution 1. Because Solution 2 has a greater molality than Solution 1 (keeping in mind that molality is the only variable in the freezing point depression equation that determines the freezing point depression), Solution 2 ends up having a greater freezing point depression than Solution 1, resulting in a Solution 2 freezing at a much lower temperature than Solution 1.
The freezing point of Solution 2 was lower than the freezing point of Solution 1 because Solution 2 contained 5 more grams of antifreeze. In the freezing point depression equation above, nothing is changed on the right-hand side of the equation except for the molality of the solute. The molal-freezing-point-constant and the van't Hoff factor remain the same. The molality changes because the moles of solute is increased. The number of moles can be determined by multiplying the number of grams by the inverted grams per mole value, which would become: grams x (moles / grams). This way, the grams would cancel out, only leaving the number of moles. Due to Solution 2 containing double the amount of grams compared to Solution 1, the moles of antifreeze in Solution 2 would be double the moles of antifreeze in Solution 1; therefore, because molality is calculated by dividing the number of moles of the solute by the mass of the solvent in kilograms, Solution 2 has a greater molality than Solution 1. Because Solution 2 has a greater molality than Solution 1 (keeping in mind that molality is the only variable in the freezing point depression equation that determines the freezing point depression), Solution 2 ends up having a greater freezing point depression than Solution 1, resulting in a Solution 2 freezing at a much lower temperature than Solution 1.
Sources of Error
Instead of using pure water, tap water was used. Tap water contains impurities, which are essentially solutes, and they can contribute to the van't Hoff factor, increasing the freezing-point depression. Therefore, the water used in this experiment should have had a freezing point of lower than 0 C because it is not pure.
The water froze at 0.1 C, which is a higher temperature than the freezing point of pure water (0 C) and the freezing point of impure water (less than 0 C). This could mean that the incremental dashes indicating differences in temperature were imprecise, skewing the data to it having slightly higher temperatures (most likely since the recorded freezing temperature of impure water was 0.1 C) or slightly lower temperatures.
When measuring the mass of the antifreeze, the balance was not checked to see if it was zeroed. Therefore, the mass of the antifreeze could be more or less than the suggested amounts. An increase in mass could increase the freezing-point depression, and a decrease in mass could decrease the freezing-point depression.
Instead of stirring the solution until it reached 0 C, the solution was continuously stirred without stopping. This prevented the freezing of the solution at the normal temperature that it would have froze. Therefore, it would have resulted in a lower freezing point of the solution.
The water froze at 0.1 C, which is a higher temperature than the freezing point of pure water (0 C) and the freezing point of impure water (less than 0 C). This could mean that the incremental dashes indicating differences in temperature were imprecise, skewing the data to it having slightly higher temperatures (most likely since the recorded freezing temperature of impure water was 0.1 C) or slightly lower temperatures.
When measuring the mass of the antifreeze, the balance was not checked to see if it was zeroed. Therefore, the mass of the antifreeze could be more or less than the suggested amounts. An increase in mass could increase the freezing-point depression, and a decrease in mass could decrease the freezing-point depression.
Instead of stirring the solution until it reached 0 C, the solution was continuously stirred without stopping. This prevented the freezing of the solution at the normal temperature that it would have froze. Therefore, it would have resulted in a lower freezing point of the solution.
Critical Thinking Analysis
1.
Molar mass of ethylene glycol (C2H4(OH)2)
2.
Solution 1 percent error
Solution 2 percent error
3.
Some of the major sources of error in this investigation are tap water being used instead of pure water, an imprecise measurement of the mass of the anitfreeze, and constant stirring of the solution. This first source of error is simple to correct. Using Fiji bottle water, the most purest water available, would fix this error. The second source of error is easy to fix also. The triple beam balance should have been zeroed in so that the scale was set at zero. The measurements should have been taken at eye level with the scale and to the nearest tenths of a gram. To be even more precise with the measurements, an electronic scale should be used so that there is essentially no room for human error. The third source of error prevented the solutions from freezing at their freezing temperature and caused them to perhaps freeze at lower temperatures because stirring prevented the solutions from solidifying as constant stirring broke the bonds trying to form to create a solid.
Some of the major sources of error in this investigation are tap water being used instead of pure water, an imprecise measurement of the mass of the anitfreeze, and constant stirring of the solution. This first source of error is simple to correct. Using Fiji bottle water, the most purest water available, would fix this error. The second source of error is easy to fix also. The triple beam balance should have been zeroed in so that the scale was set at zero. The measurements should have been taken at eye level with the scale and to the nearest tenths of a gram. To be even more precise with the measurements, an electronic scale should be used so that there is essentially no room for human error. The third source of error prevented the solutions from freezing at their freezing temperature and caused them to perhaps freeze at lower temperatures because stirring prevented the solutions from solidifying as constant stirring broke the bonds trying to form to create a solid.
Critical Thinking Applications
1. Freezing point depression could not be used for substances not soluble in water. The freezing point depression equation is the change in freezing point equal to the molal-freezing-point-depression constant times the molality of the solute times the van't Hoff factor of the solute. Since the substances are not soluble in water, the van't Hoff factor, i, would equal 1 because insoluble substances in water do not dissociate. They do not break up into smaller particles, resulting in i = 1. The molal-freezing-point-depression constant is unique only to the solvent, which in this case would be water, and it would be -1.86 C x kg / mol. The molality is of the solute, and it would essentially be 0. Molality is the number of moles of the solute that are dissolved into the solvent divided by the mass in kilograms of the solvent. Since insoluble substances do not dissolve in water, they have a molality of 0. Because molality is 0, the other values of the other variables do not matter, and the change in freezing point is 0; therefore, freezing point depression could not be used for substances not soluble in water.
2. A 1 molal solution of the ionic substance (NH4)3PO4 would still have an impact on the freezing point depression of water. The freezing point depression equation is the change in freezing point equal to the molal-freezing-point-depression constant times the molality of the solute times the van't Hoff factor of the solute. The van't Hoff factor, i, would equal 4 because the ionic substance would dissociate into 4 ions. They break up into 4 smaller particles, resulting in i = 4. The molal-freezing-point-depression constant is unique only to the solvent, which in this case would be water, and it would be -1.86 C x kg / mol. The molality is of the solute, and it is the number of moles of the solute that are dissolved into the solvent divided by the mass in kilograms of the solvent. Since the molality is 1, molality does not have an effect on the change in the freezing point. However, the van't Hoff factor significantly increases the change in the freezing point temperature because it is i = 4. The molal-freezing-point-depression constant and the molality is basically multiplied 4 times, resulting in the change in the freezing point would being lowered by 7.44 C. If the molality was greater than 1, the change in the freezing point would be much greater also, resulting in a lower freezing point.
2. A 1 molal solution of the ionic substance (NH4)3PO4 would still have an impact on the freezing point depression of water. The freezing point depression equation is the change in freezing point equal to the molal-freezing-point-depression constant times the molality of the solute times the van't Hoff factor of the solute. The van't Hoff factor, i, would equal 4 because the ionic substance would dissociate into 4 ions. They break up into 4 smaller particles, resulting in i = 4. The molal-freezing-point-depression constant is unique only to the solvent, which in this case would be water, and it would be -1.86 C x kg / mol. The molality is of the solute, and it is the number of moles of the solute that are dissolved into the solvent divided by the mass in kilograms of the solvent. Since the molality is 1, molality does not have an effect on the change in the freezing point. However, the van't Hoff factor significantly increases the change in the freezing point temperature because it is i = 4. The molal-freezing-point-depression constant and the molality is basically multiplied 4 times, resulting in the change in the freezing point would being lowered by 7.44 C. If the molality was greater than 1, the change in the freezing point would be much greater also, resulting in a lower freezing point.
3. The assumption is made that the density of distilled water in this investigation is 1 g / 1 mL, the density of pure water. The density of water was used to convert the volume of water to grams of water. The determined grams of water was used to find the number of grams of antifreeze per 1000 grams of solvent and the molar mass. If the density of water is not 1 g / 1 mL, then these calculated values based on the density of water being 1 g / 1 mL is incorrect.
4. This method of molar mass determination would be practical for other substances soluble in water. Because soluble substances have molality, once the change in freezing point has been found, finding the molality will be simple. The volume of water, the solvent, used must be converted into grams. Then, using a proportion of the grams of solute used in the experiment divided by the grams of solvent used in the experiment equal to the the amount of grams of the solute per 1000 g, or 1 kg, of water, the amount of grams of the solute per 1000 g can be determined. This value divided by the molality, which has the units of moles of the solute divided by the mass of the solvent, can determine the molar mass since the kg units cancel each other out, and only the grams over mole units are left. This process is not specific to only antifreeze because it does not depend on its chemical properties. It only depends on the substances solubility, molality, and mass. All soluble substances should have these values, so this method would be practical for other substances soluble in water.
4. This method of molar mass determination would be practical for other substances soluble in water. Because soluble substances have molality, once the change in freezing point has been found, finding the molality will be simple. The volume of water, the solvent, used must be converted into grams. Then, using a proportion of the grams of solute used in the experiment divided by the grams of solvent used in the experiment equal to the the amount of grams of the solute per 1000 g, or 1 kg, of water, the amount of grams of the solute per 1000 g can be determined. This value divided by the molality, which has the units of moles of the solute divided by the mass of the solvent, can determine the molar mass since the kg units cancel each other out, and only the grams over mole units are left. This process is not specific to only antifreeze because it does not depend on its chemical properties. It only depends on the substances solubility, molality, and mass. All soluble substances should have these values, so this method would be practical for other substances soluble in water.