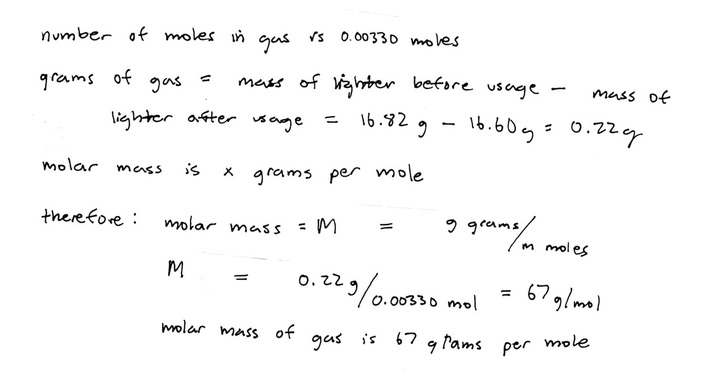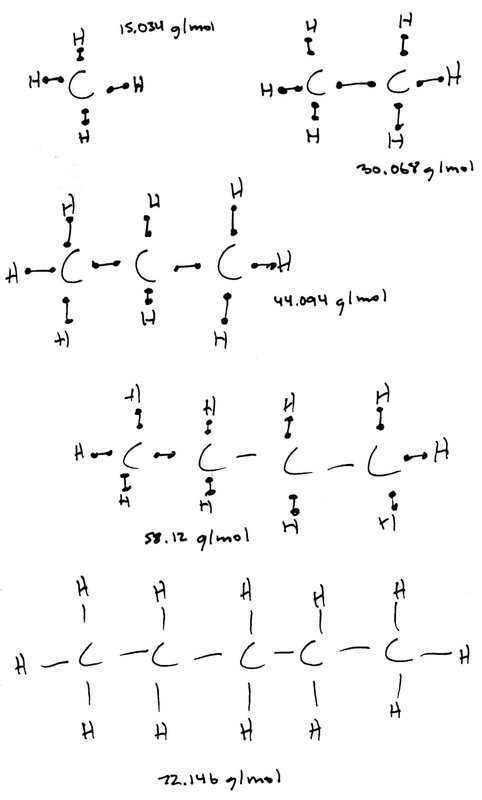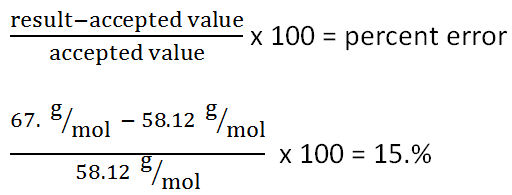Collecting a Gas Over Water Lab
Procedure
1. The three given hints are as follows: assume the gas acts like an ideal gas, assume the atmospheric pressure in the room is standard pressure, and a chart of water vapor pressures at various temperatures is provided at the lab station. The equipment that can be used for the lab is as follows: a calibrated triple beam balance, a glass bottle with a cap, a large plastic tub, a thermometer, and a graduated cylinder.
2. Be sure to record all measurements and calculations made. Fill the large plastic tub about three-fourths of the way with water. Measure the temperature of the air using the thermometer. Then, measure the temperature of the water using the thermometer.
3. Using the triple beam balance, determine the weight of the empty glass bottle with the cap. With water, completely fill the glass bottle with the cap, and determine its weight. Note that the cap is included in these measurements. Determine the volume of water that can fit in the glass bottle by using a graduated cylinder. Pour the water from the glass bottle into the graduated cylinder. Measure the mass of the lighter using the triple beam balance.
4. Ask the teacher if all of the correct measurements were made, and ask for permission to move on to the next step.
5. Drop the glass bottle in the tub filled with water. Make sure that the glass bottle is completely submerged and filled with water. Then, place the lighter underwater. Holding the opening of the completely filled bottle over the lighter’s mouth, press the button on the lighter, not the metal rotating mechanism, to release the gas in the lighter. The gas will leave the lighter in bubbles. Be sure to catch these bubbles in the glass bottle. The gases will slowly replace the water in the glass bottle.
6. After about filling the glass bottle about one-third of the way with the gas, seal it with the cap underwater. Note that the opening of the glass bottle should be always pointed downwards so that no gas escapes.
7. Measure the mass of the sealed glass bottle using the triple beam balance, and measure the volume of the water left in the sealed glass bottle using the graduated cylinder. Then, dry the wet lighter using paper towels and place it off to the side to dry. Do not push the button on the lighter as it will release gas and skew the data.
8. After the lighter has completely dried, measure the mass of the lighter using the triple beam balance. Subtract the mass of the lighter before the experiment and the mass of the lighter after the experiment to get the mass of the gas that entered the glass bottle.
9. Determine the pressure of the gas by using Dalton’s Law of Partial Pressures. Convert the total pressure (refer to step 1) into millimeters of mercury. Subtract the pressure of water vapor (refer to step 1) from the total pressure. The remainder is the pressure of the gas in millimeters of mercury.
10. Use the ideal gas law (refer to step 1), PV=nRT where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is the temperature, to determine the number of moles of gas that left the lighter. Note that the volume of the gas must be converted into liters form milliliters, the temperature must be converted into Kelvin from Celsius, the pressure is in millimeters of mercury, and the particular gas constant must be in association with millimeters of mercury.
11. To find the molar mass of the gas, divide the mass of the gas that entered the glass bottle by the calculated moles of the gas.
2. Be sure to record all measurements and calculations made. Fill the large plastic tub about three-fourths of the way with water. Measure the temperature of the air using the thermometer. Then, measure the temperature of the water using the thermometer.
3. Using the triple beam balance, determine the weight of the empty glass bottle with the cap. With water, completely fill the glass bottle with the cap, and determine its weight. Note that the cap is included in these measurements. Determine the volume of water that can fit in the glass bottle by using a graduated cylinder. Pour the water from the glass bottle into the graduated cylinder. Measure the mass of the lighter using the triple beam balance.
4. Ask the teacher if all of the correct measurements were made, and ask for permission to move on to the next step.
5. Drop the glass bottle in the tub filled with water. Make sure that the glass bottle is completely submerged and filled with water. Then, place the lighter underwater. Holding the opening of the completely filled bottle over the lighter’s mouth, press the button on the lighter, not the metal rotating mechanism, to release the gas in the lighter. The gas will leave the lighter in bubbles. Be sure to catch these bubbles in the glass bottle. The gases will slowly replace the water in the glass bottle.
6. After about filling the glass bottle about one-third of the way with the gas, seal it with the cap underwater. Note that the opening of the glass bottle should be always pointed downwards so that no gas escapes.
7. Measure the mass of the sealed glass bottle using the triple beam balance, and measure the volume of the water left in the sealed glass bottle using the graduated cylinder. Then, dry the wet lighter using paper towels and place it off to the side to dry. Do not push the button on the lighter as it will release gas and skew the data.
8. After the lighter has completely dried, measure the mass of the lighter using the triple beam balance. Subtract the mass of the lighter before the experiment and the mass of the lighter after the experiment to get the mass of the gas that entered the glass bottle.
9. Determine the pressure of the gas by using Dalton’s Law of Partial Pressures. Convert the total pressure (refer to step 1) into millimeters of mercury. Subtract the pressure of water vapor (refer to step 1) from the total pressure. The remainder is the pressure of the gas in millimeters of mercury.
10. Use the ideal gas law (refer to step 1), PV=nRT where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is the temperature, to determine the number of moles of gas that left the lighter. Note that the volume of the gas must be converted into liters form milliliters, the temperature must be converted into Kelvin from Celsius, the pressure is in millimeters of mercury, and the particular gas constant must be in association with millimeters of mercury.
11. To find the molar mass of the gas, divide the mass of the gas that entered the glass bottle by the calculated moles of the gas.
Data
Temperature of air: 25.1 oC
Temperature of water: 23.0 oC
Mass of bottle full of air: 213.55 g
Mass of bottle full of water: 477.51 g
Mass of bottle full of water and gases: 362.62 g
Mass of lighter before usage: 16.82 g
Mass of lighter after usage: 16.60 g
Volume of water in bottle full of water: 263.5 mL
Volume of water in bottle full of water and gases: 181.1 mL
Pressure of water vapor: 21 mmHg
Pressure of room where lab was done: 1 atm
Calculated pressure of gas: 739. mmHg
Calculated moles of gas: 0.00330 mol
Calculated molar mass of gas: 67 g/mol
Temperature of water: 23.0 oC
Mass of bottle full of air: 213.55 g
Mass of bottle full of water: 477.51 g
Mass of bottle full of water and gases: 362.62 g
Mass of lighter before usage: 16.82 g
Mass of lighter after usage: 16.60 g
Volume of water in bottle full of water: 263.5 mL
Volume of water in bottle full of water and gases: 181.1 mL
Pressure of water vapor: 21 mmHg
Pressure of room where lab was done: 1 atm
Calculated pressure of gas: 739. mmHg
Calculated moles of gas: 0.00330 mol
Calculated molar mass of gas: 67 g/mol
Calculations
Volume of gas:
Volume of water in bottle full of water - Volume of water in bottle full of water and gases = Volume of gases in bottle full of water and gases
263.5 mL - 181.1 mL = 82.4 mL
Mass of gas:
Mass of lighter before usage - Mass of lighter after usage = Mass of gas
16.82 g - 16.60 g = 0.22 g
Temperature of water in Kelvin:
Temperature of water in Celsius + 273 = Temperature of water in Kelvin
23.0 oC + 273 = 296 K
Volume of water in bottle full of water - Volume of water in bottle full of water and gases = Volume of gases in bottle full of water and gases
263.5 mL - 181.1 mL = 82.4 mL
Mass of gas:
Mass of lighter before usage - Mass of lighter after usage = Mass of gas
16.82 g - 16.60 g = 0.22 g
Temperature of water in Kelvin:
Temperature of water in Celsius + 273 = Temperature of water in Kelvin
23.0 oC + 273 = 296 K
Pressure of gas:
Moles of gas:
Molar mass of gas:
Conclusion
The primary objective of this lab was to find the molar mass of the lighter gas. The temperature of the water is 23.0 oC. On the provided chart, the water vapor pressure at 23.0 oC is 21.0 mmHg. The mass of the lighter before usage is 16.82 g, and the mass of the lighter after usage is 16.60 g; therefore, the mass of the gas that left the lighter and entered the glass bottle is 0.20 g. The volume of water in the bottle full of water is 263.5 mL, the volume of water in the bottle full of water and gases is 181.1 mL, and the volume of gases in the bottle full of water and gases is 82.4 mL. Since it is assumed that the total pressure is 1 atm - using Dalton’s Law of Partial Pressures - the pressure of the gas can be determined by subtracting the total pressure by the pressure of water vapor. The pressure of the gas turns out to be 739. mmHg. The total pressure is not solely the gas from the lighter because there is always water vapor present over liquid water, so this calculation must be made. Since it is assumed that the gas behaves like an ideal gas, the ideal gas law can be used to find moles, which is 0.00330 mol. The molar mass’s units is grams per mole, so the molar mass can be determined by dividing the grams, the difference in mass between the before and after masses of the lighter which is 0.20 g, by the moles which is 0.00330 mol. The molar mass comes out to be 67. grams per mole. It is "about" 67. g/mol because there were multiple sources of error. Some of the gas bubbles did not enter the glass bottle, some water stuck to the sides of the glass bottle when transferring the water to the graduated cylinder to be measured, and the lighter was not completely dry when measuring its mass after the experiment.
Analysis
1. Based on the calculations, the molar mass of the gas is 67. g/mol.
2. The gas is alkane, meaning that it contains only carbon and hydrogen with single bonds. The calculated molar mass is 67. g/mol. The molar mass of carbon is 12.01 g/mol, and the molar mass of hydrogen is 1.008 g/mol. Carbon and hydrogen make up covalent bonds, meaning that they share electrons. Starting out with using only one carbon and three hydrogens, carbon and two hydrogens were repeatedly added until a molar mass which was the most similar to the calculated molar mass was reached. The most similar molar mass to the calculated molar mass was at 72.146 g/mol, having 5 carbons and 12 hydrogens. The formula for the gas would be C5H12.
2. The gas is alkane, meaning that it contains only carbon and hydrogen with single bonds. The calculated molar mass is 67. g/mol. The molar mass of carbon is 12.01 g/mol, and the molar mass of hydrogen is 1.008 g/mol. Carbon and hydrogen make up covalent bonds, meaning that they share electrons. Starting out with using only one carbon and three hydrogens, carbon and two hydrogens were repeatedly added until a molar mass which was the most similar to the calculated molar mass was reached. The most similar molar mass to the calculated molar mass was at 72.146 g/mol, having 5 carbons and 12 hydrogens. The formula for the gas would be C5H12.
3. Based on the fact that most of the gas in the lighter is butane: C4H10, which has a molar mass 58.12 g/mol, the percent error would be 15.%.
4. A. If the change from Celsius temperature to Kelvin was forgotten, the value of the calculated molar mass would be lower. The ideal gas law, PV=nRT, requires the temperature in units of Kelvin. If the temperature was left in Celsius, which is 273 degrees lower than Kelvin, it would have caused the number of moles to be dramatically higher because PV is being divided by a much smaller number. Since the number of grams is being divided by a larger number of moles, the molar mass would be lower.
B. If the inclusion of the pressure of water vapor was forgotten, the value of the calculated molar mass would be lower. There would be no need to use Dalton’s Law of Partial Pressures since the pressure of the gas is the total pressure. Therefore, the pressure of the gas would be higher since nothing else is being added to it to make the total pressure; the pressure itself is the total pressure. Since the pressure used in the ideal gas law is higher, the number of moles would be higher since PV is greater than it should be. Since the number of grams is being divided by a larger number of moles, the molar mass would be lower.
C. If there were air bubbles in the glass bottle before releasing the lighter gas into it, the value of the calculated molar mass would become higher. There would be many more gases involved than just the lighter gas and water vapor; if air was in the bottle, there would be nitrogen, oxygen, argon, carbon dioxide, and many more gases. The sum of all of these gases would be 1 atm; therefore, since gases that form air were considered in Dalton’s Law of Partial Pressures, the pressure of the lighter gas would be lower, which would cause the P, pressure, in the ideal gas law, PV=nRT, to be lower also. The number of moles would be lower since PV is lower than it should be. Since the number of grams is being divided by a smaller number of moles, the molar mass would become higher.
D. If the lighter was not completely dry the when weighed the second time, the value of the calculated molar mass would become lower. The weight of the lighter after being measured the second time would be the mass of the lighter plus the mass of the remaining water drying off. Since the grams of lighter gas that left the lighter is calculated by subtracting the weight of the lighter after the experiment and the weight of the lighter before the experiment, the grams of lighter gas that left the lighter would be lower; therefore, because molar mass is calculated by dividing moles from grams, the decrease in grams would cause the molar mass to become lower.
5. Based on the results, the other gases have a higher molar mass than butane. The molar mass of butane is 58.12 g/mol, but the calculated molar mass for butane is 67. g/mol. Originally, the idea that there were really several gases mixed together in the lighter fluid was unknown. Before, it was thought to be that the liquid was mainly butane. Since acquiring this knowledge, it makes sense that 67. g/mol is the molar mass of the lighter fluid - there were other gases besides butane. These other gases must have an extremely large molar mass because they comprise about 8.88 g/mol and take less space than butane. It was said that most of the gas in the lighter was butane. Because this value is so large and the amount is so little, these other gases have a higher molar mass than butane.
6. The lighter fluid is composed of many gases but is mainly butane. The fluid is a gas at a pressure of 1 atm. The lighter fluid is a fluid inside the lighter because it is under extremely high pressure. This pressure causes a phase change; the gas changes into a fluid. When the button is pressed to release the fluid, the large difference in pressure (the lighter has much higher pressure than outside of the lighter) causes the fluid to phase change into a gas as it rapidly diffuses out of the lighter.
B. If the inclusion of the pressure of water vapor was forgotten, the value of the calculated molar mass would be lower. There would be no need to use Dalton’s Law of Partial Pressures since the pressure of the gas is the total pressure. Therefore, the pressure of the gas would be higher since nothing else is being added to it to make the total pressure; the pressure itself is the total pressure. Since the pressure used in the ideal gas law is higher, the number of moles would be higher since PV is greater than it should be. Since the number of grams is being divided by a larger number of moles, the molar mass would be lower.
C. If there were air bubbles in the glass bottle before releasing the lighter gas into it, the value of the calculated molar mass would become higher. There would be many more gases involved than just the lighter gas and water vapor; if air was in the bottle, there would be nitrogen, oxygen, argon, carbon dioxide, and many more gases. The sum of all of these gases would be 1 atm; therefore, since gases that form air were considered in Dalton’s Law of Partial Pressures, the pressure of the lighter gas would be lower, which would cause the P, pressure, in the ideal gas law, PV=nRT, to be lower also. The number of moles would be lower since PV is lower than it should be. Since the number of grams is being divided by a smaller number of moles, the molar mass would become higher.
D. If the lighter was not completely dry the when weighed the second time, the value of the calculated molar mass would become lower. The weight of the lighter after being measured the second time would be the mass of the lighter plus the mass of the remaining water drying off. Since the grams of lighter gas that left the lighter is calculated by subtracting the weight of the lighter after the experiment and the weight of the lighter before the experiment, the grams of lighter gas that left the lighter would be lower; therefore, because molar mass is calculated by dividing moles from grams, the decrease in grams would cause the molar mass to become lower.
5. Based on the results, the other gases have a higher molar mass than butane. The molar mass of butane is 58.12 g/mol, but the calculated molar mass for butane is 67. g/mol. Originally, the idea that there were really several gases mixed together in the lighter fluid was unknown. Before, it was thought to be that the liquid was mainly butane. Since acquiring this knowledge, it makes sense that 67. g/mol is the molar mass of the lighter fluid - there were other gases besides butane. These other gases must have an extremely large molar mass because they comprise about 8.88 g/mol and take less space than butane. It was said that most of the gas in the lighter was butane. Because this value is so large and the amount is so little, these other gases have a higher molar mass than butane.
6. The lighter fluid is composed of many gases but is mainly butane. The fluid is a gas at a pressure of 1 atm. The lighter fluid is a fluid inside the lighter because it is under extremely high pressure. This pressure causes a phase change; the gas changes into a fluid. When the button is pressed to release the fluid, the large difference in pressure (the lighter has much higher pressure than outside of the lighter) causes the fluid to phase change into a gas as it rapidly diffuses out of the lighter.